09. Probabilistic Roadmap Exercise
Probabilistic Roadmap
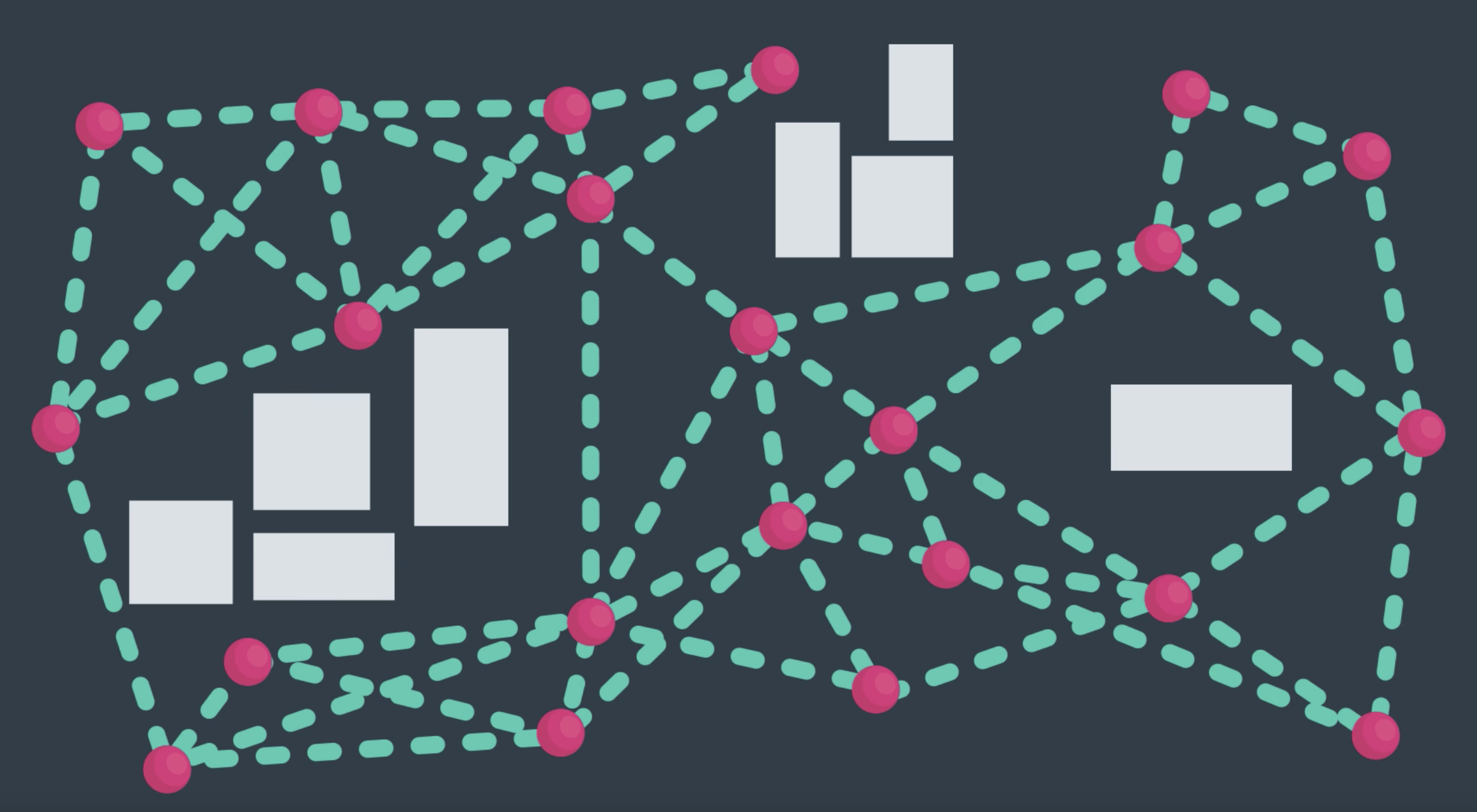
In the previous random sampling exercise, you saw that with the Python shapely library it's relatively easy to cast your obstacles as polygon objects and test for collision with points in a 2D plane. Then, by comparing the height of the obstacle with the z-dimension of the point in question, you could discard states in collision and retain all candidate states in free space.
In this exercise, you'll connect the states that you've randomly sampled to create a graph representation of the free space in the environment. After that, you'll run search to find a path through this graph from start to goal!
KD Trees
In the last exercise, you saw that naively checking for collision between all points and all object polygons can be slow. We hinted there that the KD Tree data structure can help to alleviate this inefficiency by allowing you to quickly identify nearest neighbors to a point or polygon.
You'll be faced with the same problem here when you attempt to connect nodes together into a graph, namely, trying to connect all nodes with all other nodes is costly and not really what you want to do anyway. So now is a good time to consider KD Trees more closely!
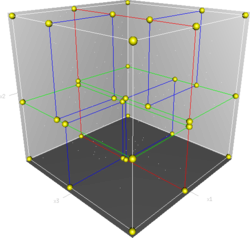
Visual of the KD Tree in action
The KD Tree is a space-partitioning data structure, which allows for fast search queries. The KD Tree achieves this by cutting the search space in half on each step of a query. If you're familiar with "big O notation", this brings the total search time down to O(m * log(n)) from O(m*n), where m is the number of elements to compare to and n is the number of elements in the KD Tree. So for example, if you want to find the closest neighbor to a single point, m=1 and n is equal to the total number of potential neighbors.
The Python Scikit-Learn (sklearn) library has an easy to use implementation of KD Trees that we'll be introducing in this exercise. To find neighbors using this implementation, you'll use it like this:
# Import KDTree and numpy
from sklearn.neighbors import KDTree
import numpy as np
# Generate some random 3-dimensional points
np.random.seed(0)
points = np.random.random((10, 3)) # 10 points in 3 dimensions
# Cast points into a KDTree data structure
tree = KDTree(points)
# Extract indices of 3 closest points
# Note: need to cast search point as a list
# and return 0th element only to get back list of indices
idxs = tree.query([points[0]], k=3, return_distance=False)[0]
# indices of 3 closest neighbors (will vary due to random sample)
print(idxs)
> [0 3 1]Probabilistic Roadmap Exercise
In this exercise, you'll perform random sampling as before, but this time using a KDTree for finding the nearest polygon. Next, you'll use networkx to generate a graph of nodes from points that lie in free space. Then you'll test pairs of nodes for connectivity through free space and determine edges for the graph. Once you have a graph of nodes and edges, you'll perform search to find a path from start to goal!
This exercise is pretty involved, but using KDTrees along with everything else you've learned in previous lessons you have all the tools for success! If you want a peek at our solution check out the link at the bottom of the notebook.
This is a modern technique and the relevant detail goes far beyond what's presented in this exercise. We wanted to give you a taste of it, but if you want to dig deeper, this article is a great starting point!
Workspace
This section contains either a workspace (it can be a Jupyter Notebook workspace or an online code editor work space, etc.) and it cannot be automatically downloaded to be generated here. Please access the classroom with your account and manually download the workspace to your local machine. Note that for some courses, Udacity upload the workspace files onto https://github.com/udacity, so you may be able to download them there.
Workspace Information:
- Default file path:
- Workspace type: jupyter
- Opened files (when workspace is loaded): n/a